A list of citations can be found here.
Edited books:
 and Waves in Geophysics. Springer (Book) (1), pp 1-195 (2022).
and Waves in Geophysics. Springer (Book) (1), pp 1-195 (2022).Published papers:
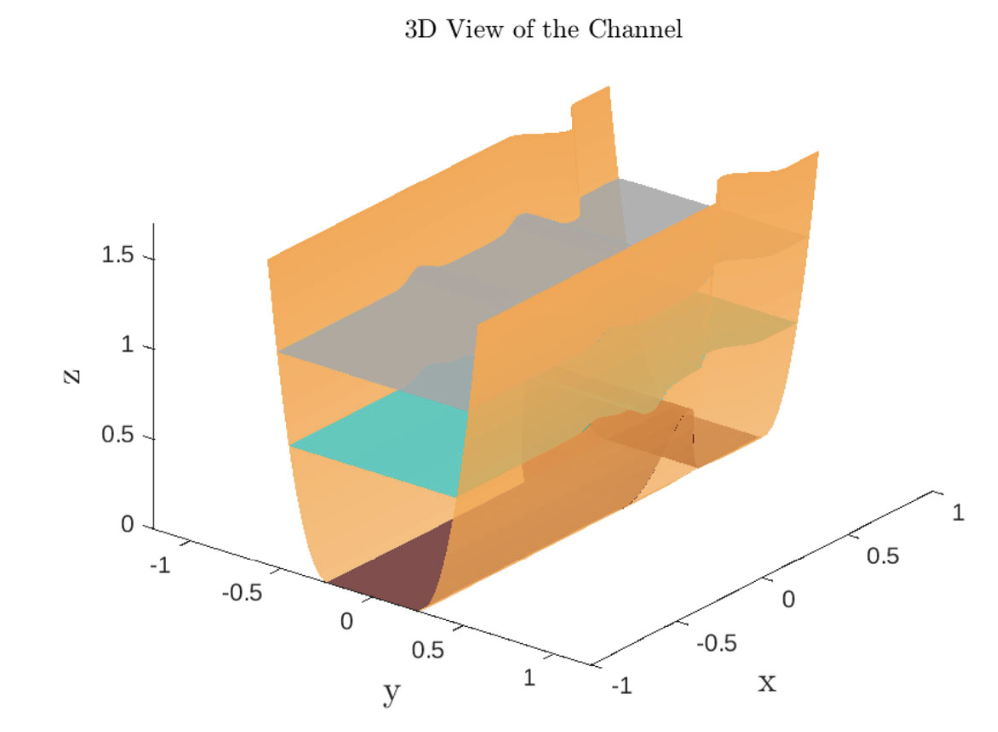
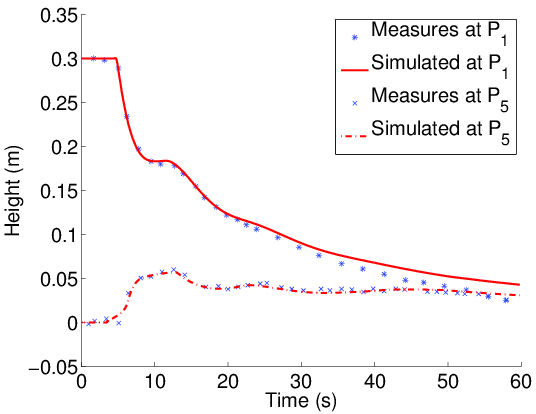
Figure: Two-layer flow in channels.

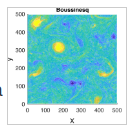
Figure: Graph of aerosols & rain.
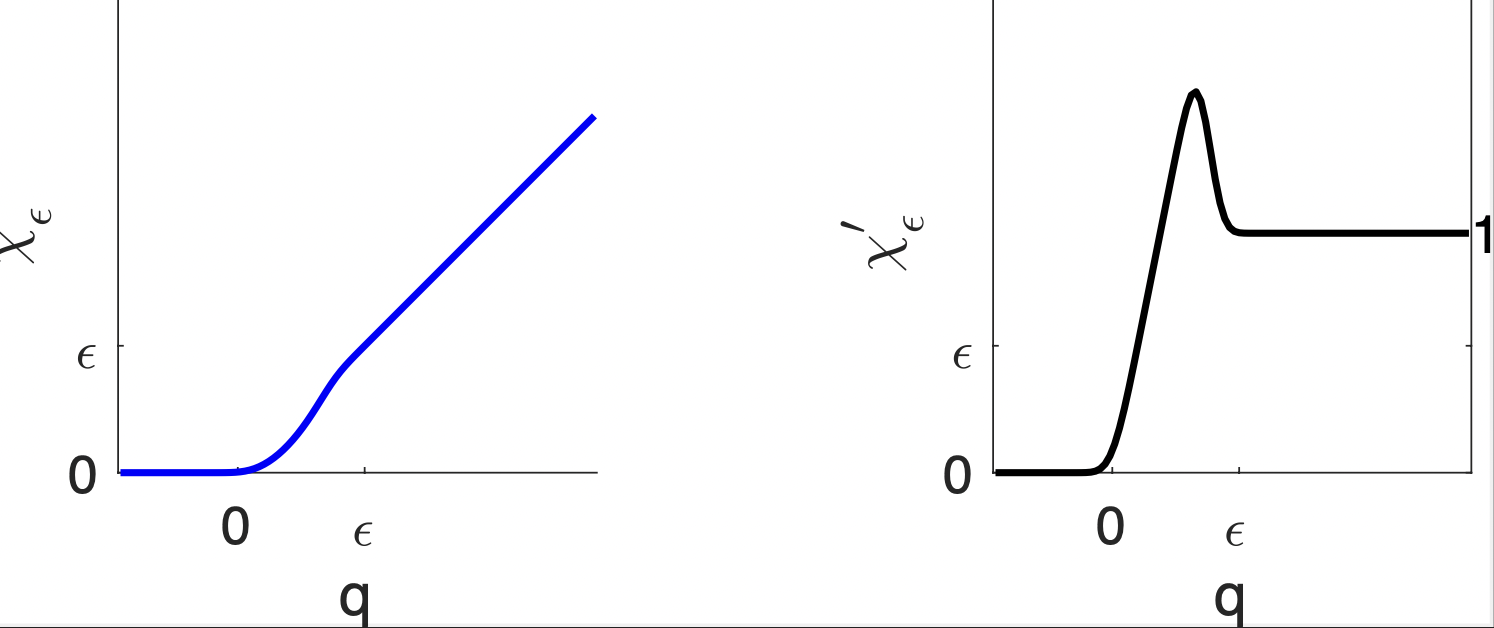
Figure: Graph of transition function from saturated to unsaturated regions.
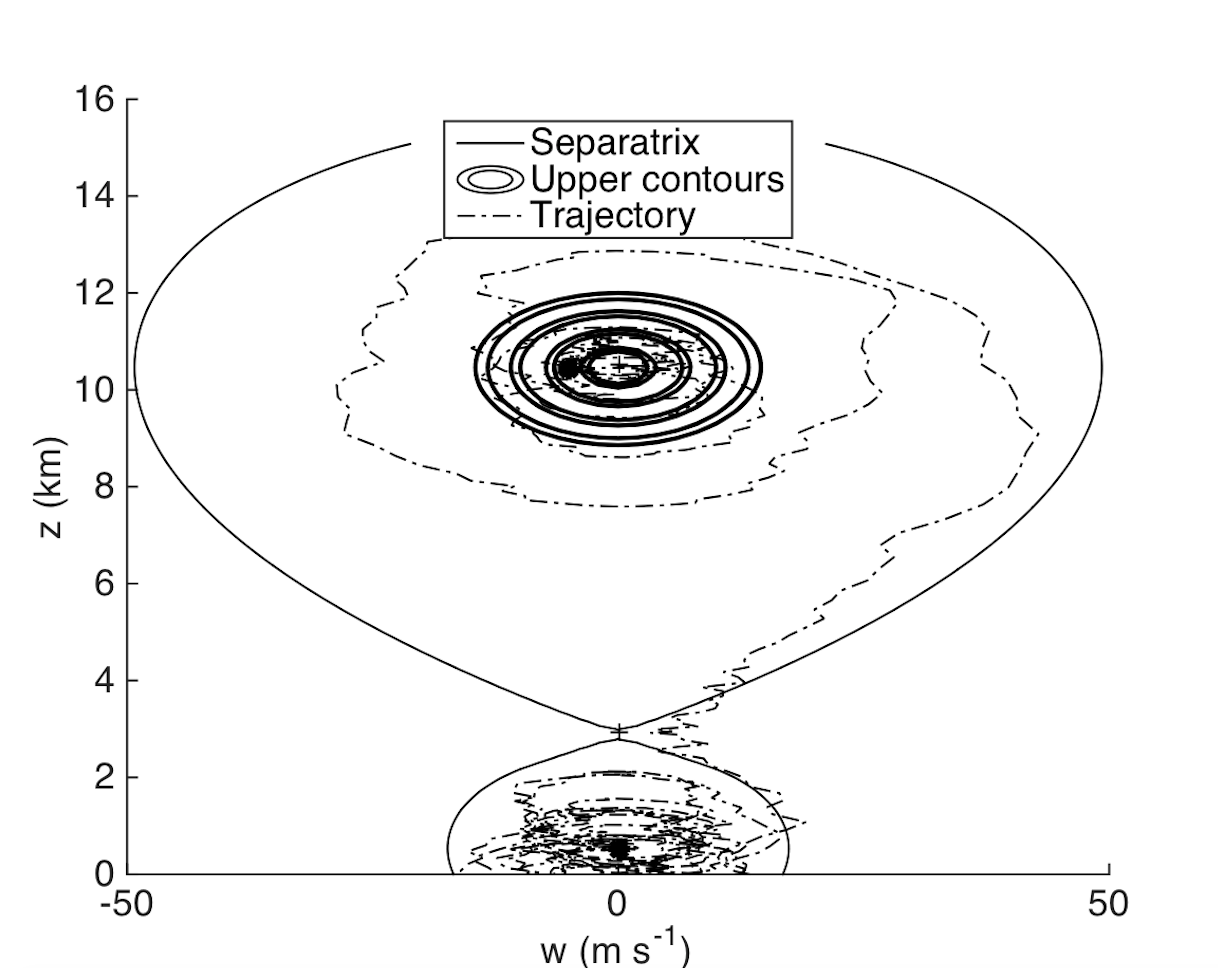 G. Hernandez-Duenas, S. Stechmann and L. Smith. Quarterly Journal of the Royal Meteorological Society (2019), Volume 145, No. 722, pp 2272-2291 (2019).
G. Hernandez-Duenas, S. Stechmann and L. Smith. Quarterly Journal of the Royal Meteorological Society (2019), Volume 145, No. 722, pp 2272-2291 (2019). 
G. Hernandez-Duenas, Ulises Velasco-García and Jorge Velasco Hernández. ESAIM: Mathematical Modelling and Numerical Analysis (2019).
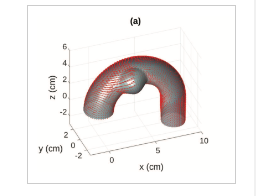
Figure: Schematic of the two-phase flows in deviated pipes.
10. A Hybrid Method to Solve Shallow Water Flows with Horizontal Density Gradients.
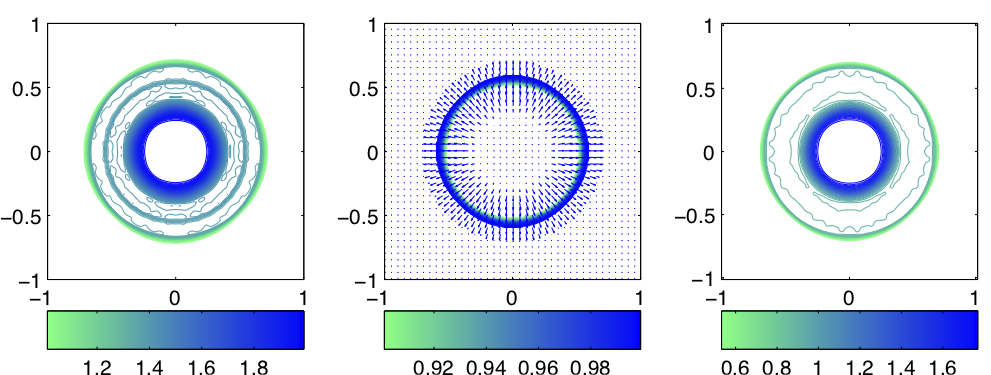 G. Hernandez-Duenas. Journal of Scientific Computing (2017), Volume 73 (2-3) pp 753-782.
G. Hernandez-Duenas. Journal of Scientific Computing (2017), Volume 73 (2-3) pp 753-782.Link to Journal
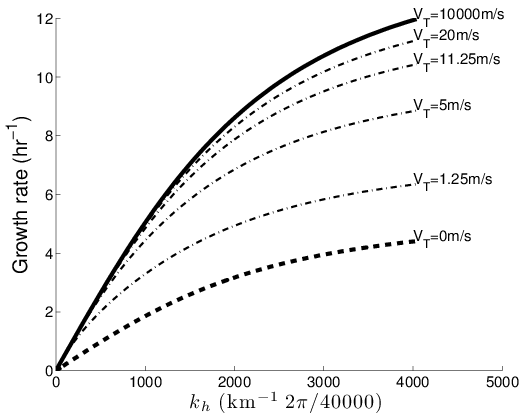
Journal of Atmospheric Sciences, Vol 72, No. 6 (2015), pp. 2379-2393
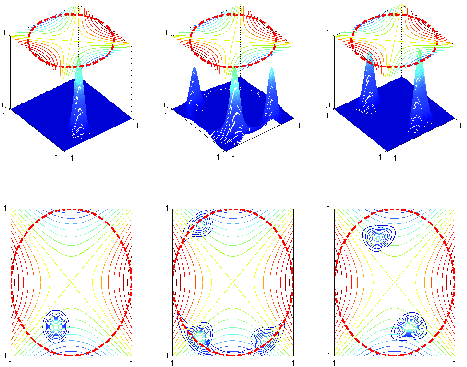
Journal of Functional Analysis, 268 no. 7 (2015), pp. 1755-1807
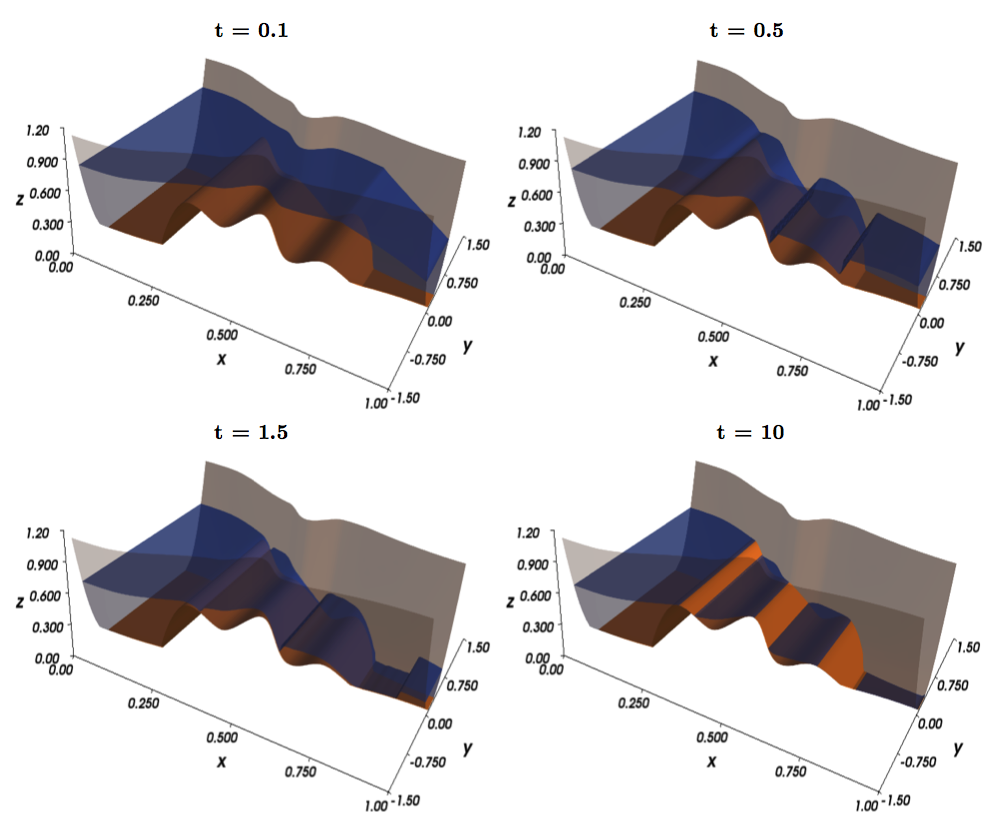
Blue: Water height. Brown: Bottom topography. Gray: Walls.
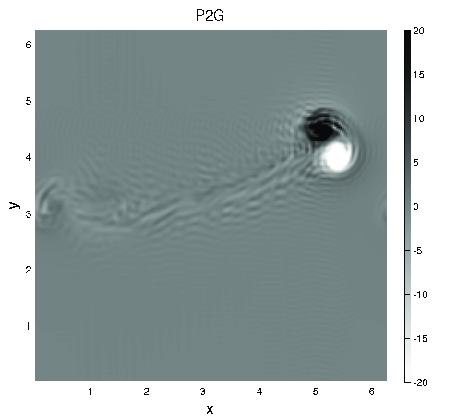
Journal of Fluid Mechanics, 747 (2014), 247-287
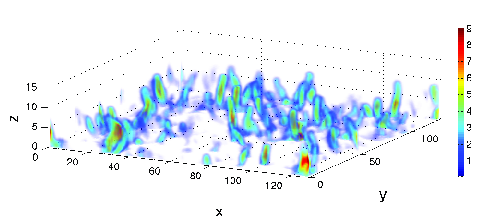
G. Hernandez-Duenas, Andrew J. Majda, Leslie M. Smith, and Samuel N. Stechmann.
Journal of Fluid Mechanics, 717 (2013), 576-611.
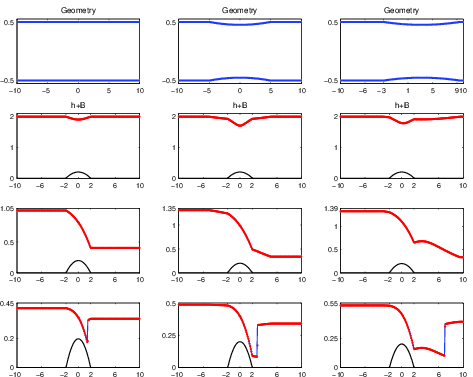
G. Hernández and Smadar Karni.
J. Sci. Comput. 48 (2011), no. 1-3, 190-208.
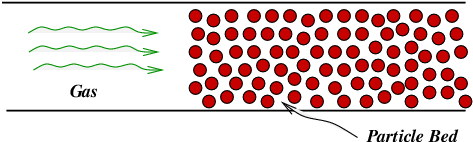
Smadar Karni and G. Hernández-Dueñas.
J Sci Comput, 45, (2010), 382-403.
1.A Hybrid Scheme for Flows in Porous Media.
Smadar Karni and G. Hernández-Dueñas.
Hyperbolic Problems: Theory, Numerics, Applications.
Proceedings of Simposia in Applied Mathematics, Volume 67, Part 2, (2009), 715-724.
Amer. Math. Soc., Providence, RI, (2009).
Submitted papers:
1. S. Shah & G.- Hernandez-Duenas. A weakly-compressible two-layer shallow water model in general channels.
Papers in preparation:
1. Jeffrey J. Early, Gerardo Hernández-Dueñas, Leslie M. Smith & M.-Pascale Lelong. Exact expressions for available potential energy and available potential vorticity.Extended abstracts:

A Scheme for Shallow Water Flow with Area Variation.
Smadar Karni and G. Hernández-Dueñas.
American Institute of Physics.
AIP Conference Proceedings
International Conference on Numerical Analysis and Applied Mathematics
Rethymno, Crete, Greece, 18-22 September 2009. 1168 (2009), 1433-1436.

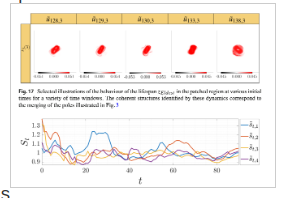
 ensional shallow water flows in open channels with varying width
ensional shallow water flows in open channels with varying width