Complete list of publications (last updated 2023/July/12):
A list of citations can be found here.
Edited books:
1. G- Hernandez-Duenas & M. A. Moreles. Mathematical and Computational Models of Flows  and Waves in Geophysics. Springer (Book) (1), pp 1-195 (2022).
and Waves in Geophysics. Springer (Book) (1), pp 1-195 (2022).
Figure: Book about Geophysical applications.
Published papers:
S. Shah & G. Hernández-Dueñas.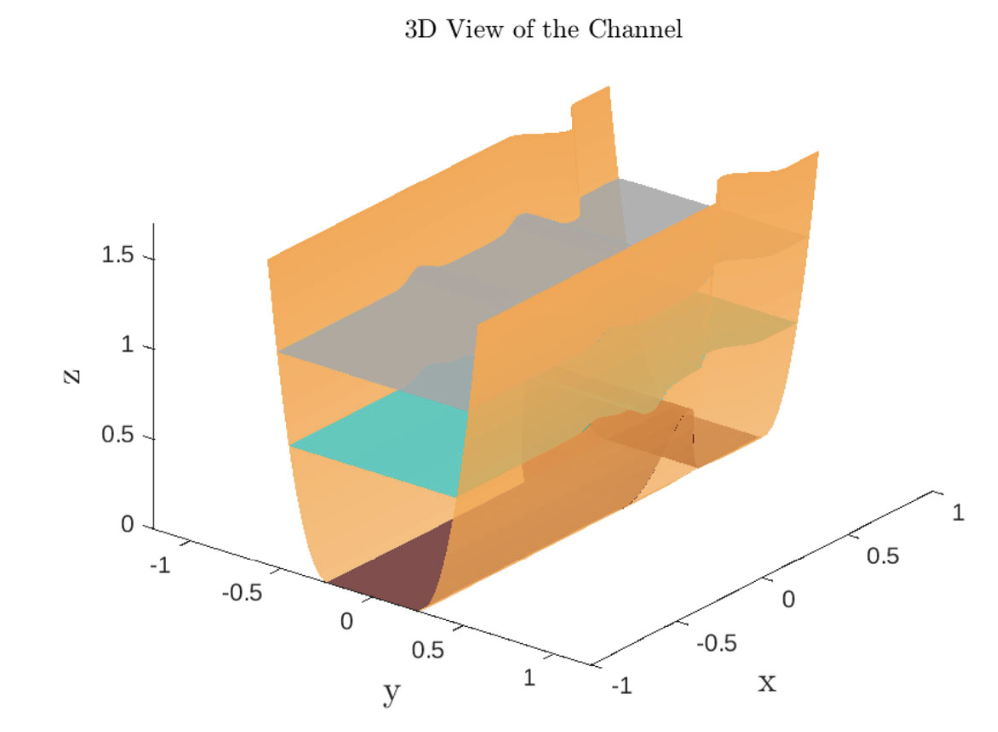
Journal of Scientific Computing (2024)
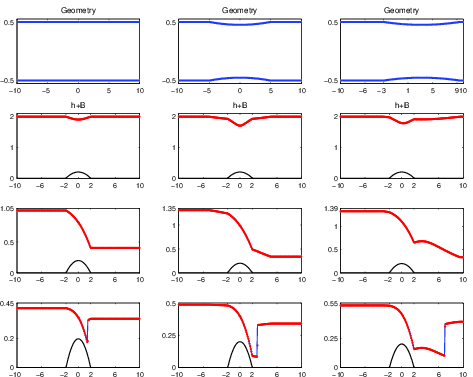
Figure: Two-layer flow in channels.
O. Guerrero-Medina & G. Hernández-Dueñas.

Physics of Fluids (2024)
Figure: Graph of aerosols & rain.
Néstor A. Sánchez-Goycochea & G.- Hernández-Dueñas.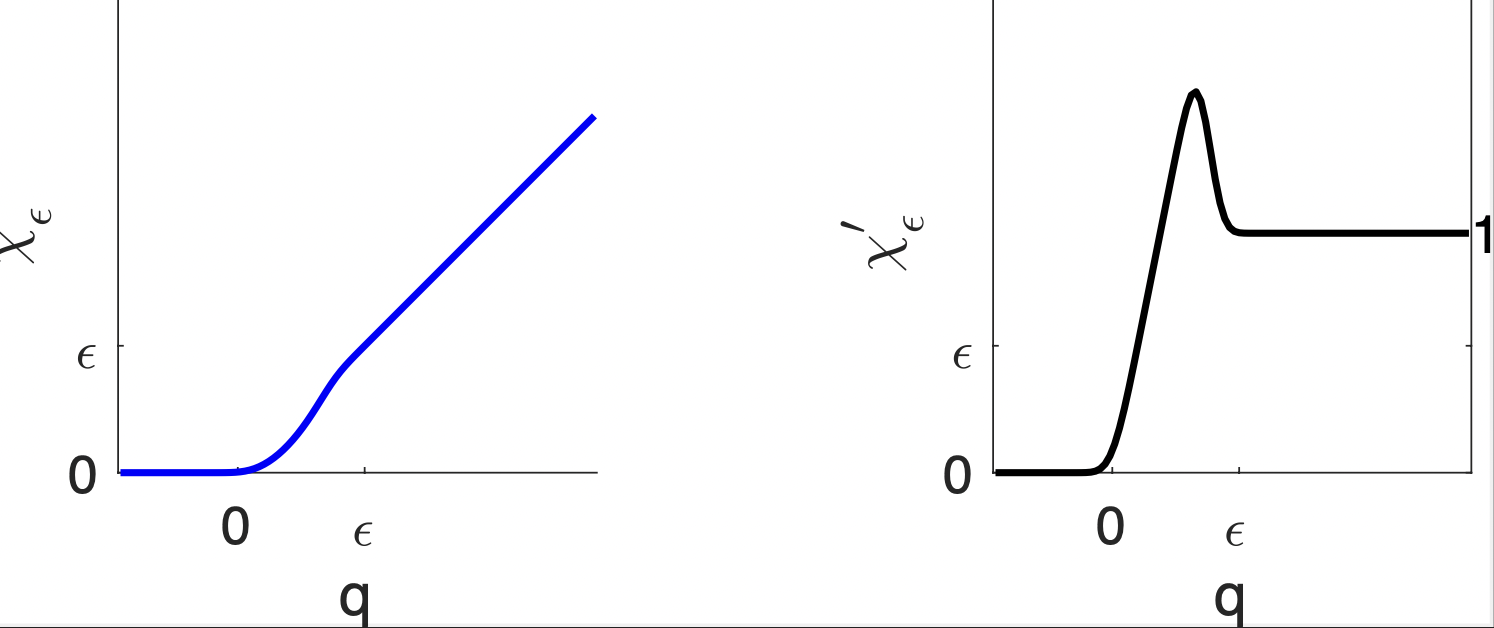
Journal of Mathematical Analysis and Applications (2024)
Figure: Graph of transition function from saturated to unsaturated regions.
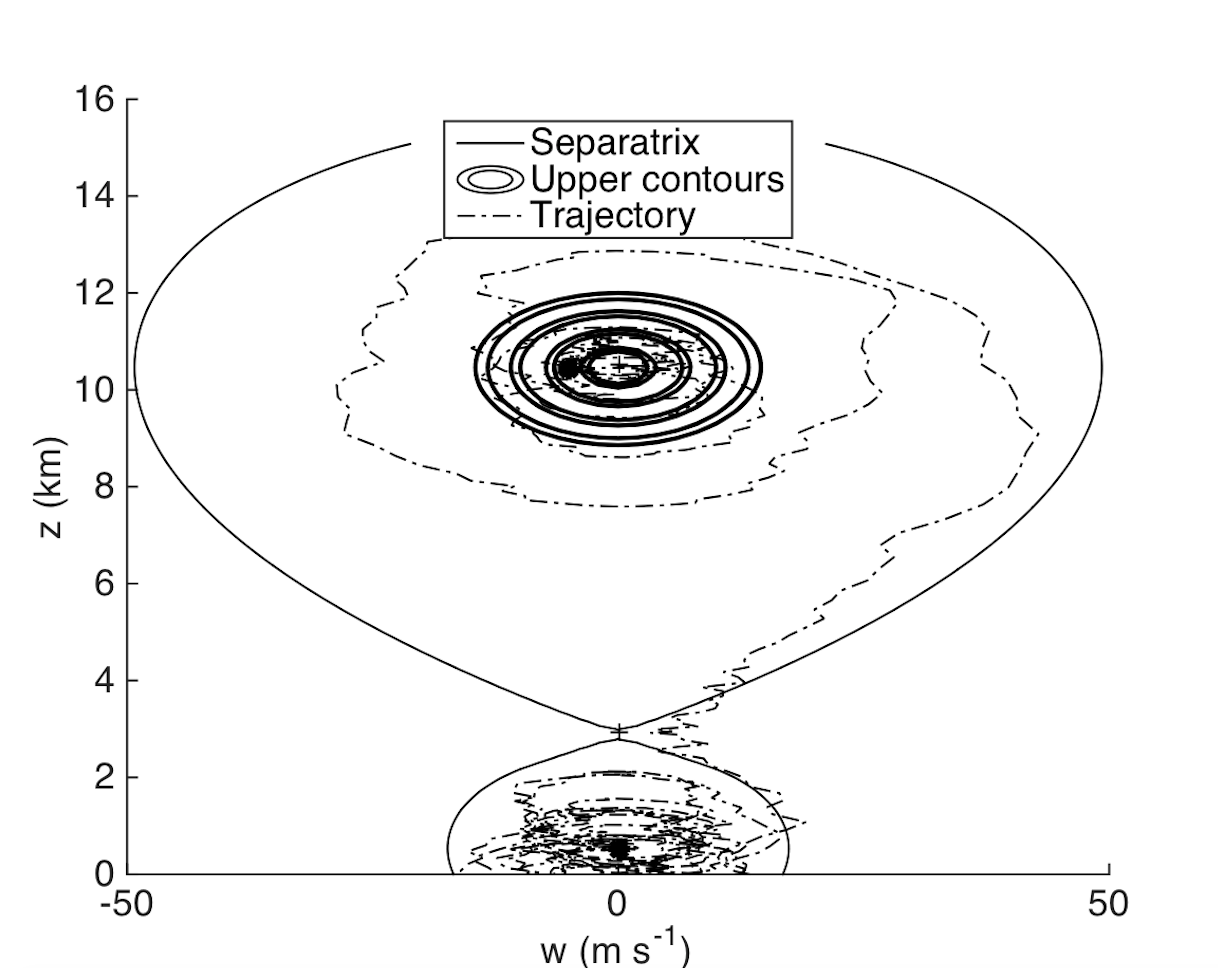
C. Blachut, C. González-Tokman & G.- Hernández-Dueñas.
Journal of Nonlinear Science (2023)
Figure: Identification of coherent structures using dynamical systems
C.A. Rosales-Alcantar & G.- Hernández-Dueñas
ESAIM: Mathematical Modeling and Numerical Analysis (2023).
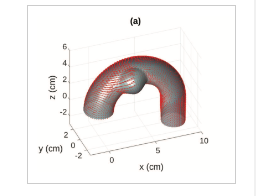
Figure: Circulation pattern in blood flow simulation
G. Hernandez-Duenas, M.A. Moreles & P. Gonzalez-Casanova
Physics of Fluids (2023)
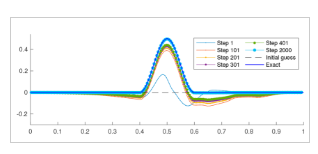
Figure: Bathymetry estimation with the steepest descent method
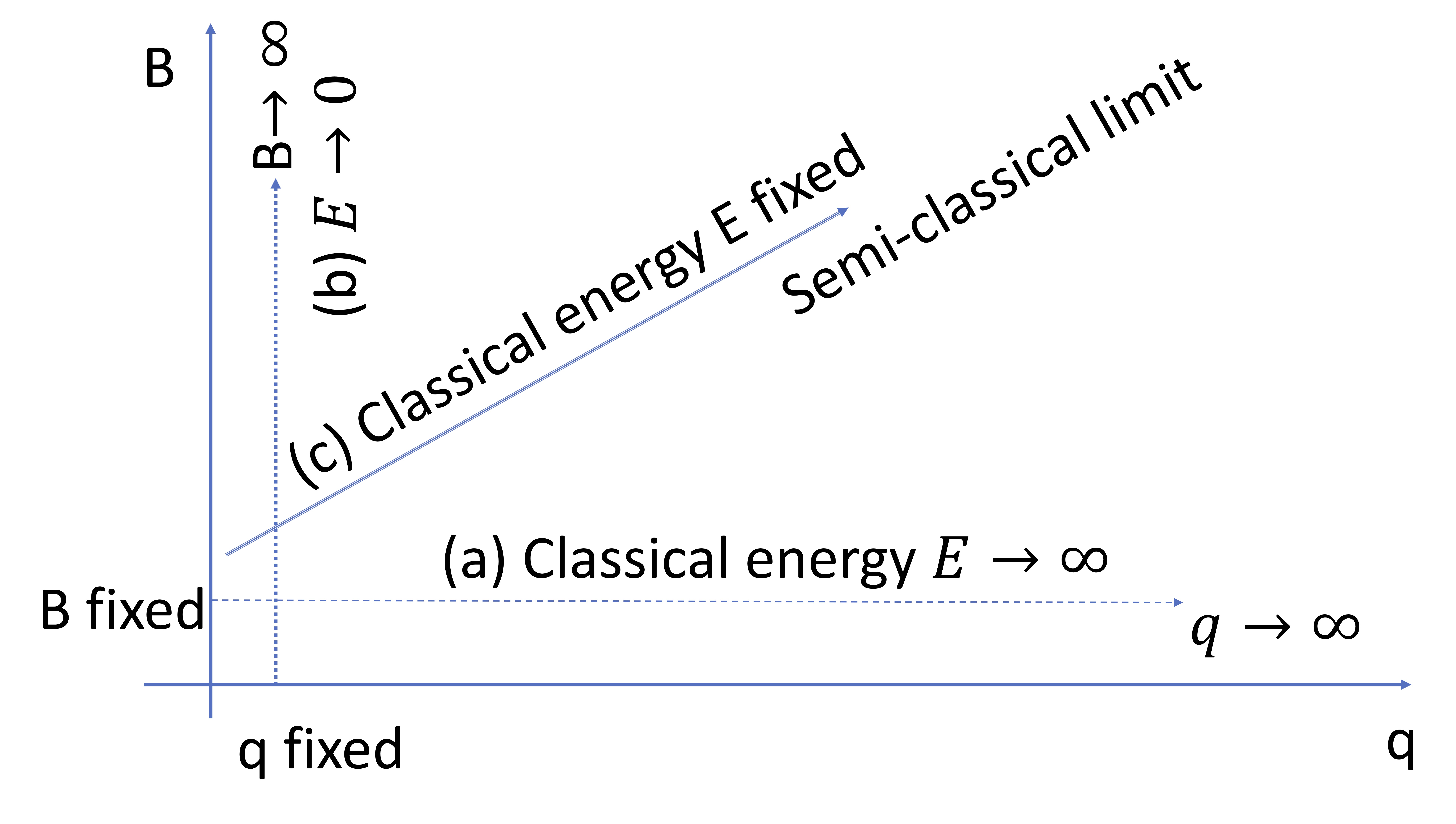
G. Hernandez-Duenas, S. Pérez-Esteva, A. Uribe & C. Villegas-Blass
Ann. Henri Poincaré (2022). https://doi.org/10.1007/s00023-021-01092-7
Figure: Diagram of different limiting regimes for the Landau problem
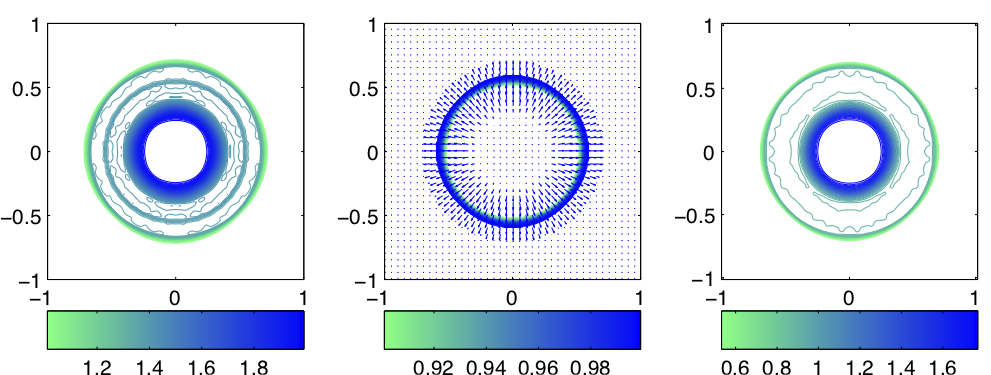
G. Hernandez-Duenas, M. Pascale Lelong, and Leslie M. Smith
Journal of Physical Oceanography (2021).
The numerical model simulations upon which this study is based are too large to archive. The velocity and density data at 200 inertial periods as well as the data for the particles' trajectories from 200 to 210 inertial periods are available here.
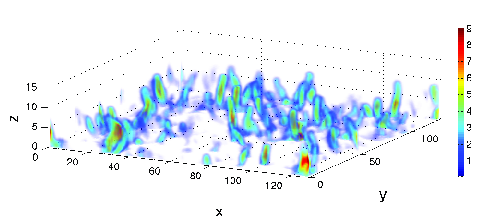
Figure: Horizontal contours of linear potential vorticity.
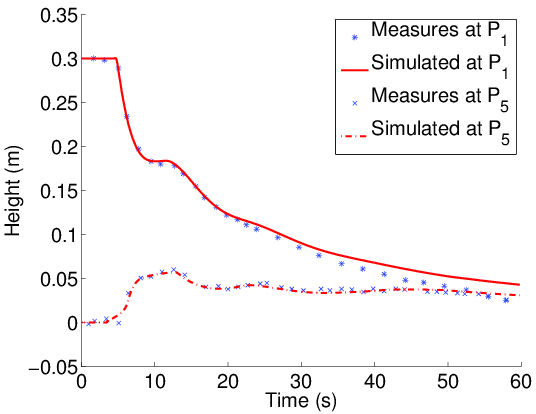
G. Hernandez-Duenas & J. Balbas
ESAIM: Mathematical Modeling and Numerical Analysis (2021).
Figure: Schematic of a two layer shallow water flow
G. Hernandez-Duenas, G. Ramirez-Santiago
Figure: Schematic for blood-flow model
Figure: Radial dam break over flat topography (height, density and pressure)
G. Hernandez-Duenas and Abdelaziz Beljadid.
Advances in Water Resources 96 (2016) 323-338.
Figure: Schematic of channel in numerical experiment of dam break.
G. Hernandez-Duenas, Leslie M. Smith, and Samuel N. Stechmann.
Journal of Atmospheric Sciences, Vol 72, No. 6 (2015), pp. 2379-2393
Figure: Growth rates versus horizontal wavenumbers for different values of rainfall speed.
G. Hernández-Dueñas and Alejandro Uribe.
Journal of Functional Analysis, 268 no. 7 (2015), pp. 1755-1807
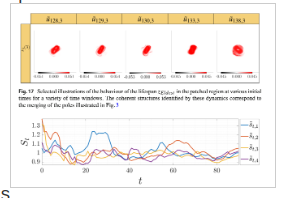
Figure: Propagation of a coherent state in a Zoll-type domain.
Jorge Balbás and G. Hernández-Dueñas.
ESIAM: Mathematical Modelling and Numerical Analysis (M2AN) 48 (2014) 665-696.
Figure: Dam break simulation at different times.
Blue: Water height. Brown: Bottom topography. Gray: Walls.
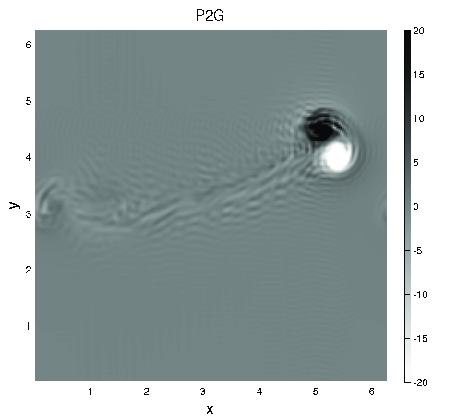
G. Hernandez-Duenas, Leslie M. Smith, and Samuel N. Stechmann
Journal of Fluid Mechanics, 747 (2014), 247-287
Figure: Dipole evolution given by the Boussinesq model
Figure: Contours of rain water. Scattered convection (left) versus squall lines (right).
Figure: Exact and numerical steady state (discontinuous transcritical) solutions to shallow water.
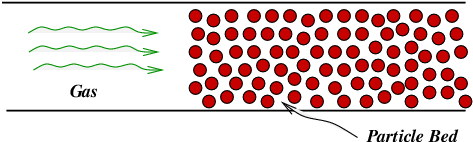
Figure 1: Schematic: Gas flow over a porous particle bed.
1.A Hybrid Scheme for Flows in Porous Media.
Smadar Karni and G. Hernández-Dueñas.
Hyperbolic Problems: Theory, Numerics, Applications.
Proceedings of Simposia in Applied Mathematics, Volume 67, Part 2, (2009), 715-724.
Amer. Math. Soc., Providence, RI, (2009).
Link to Journal
Submitted papers:
1. S. Shah & G.- Hernandez-Duenas. A weakly-compressible two-layer shallow water model in general channels.
2. O. Guerrero-Medina & G. Hernandez-Dueñas. Exploring the excess of cloud condensation nuclei and rain suppression using a minimal 3D Boussinesq model with bulk cloud microphysics.
Papers in preparation:
1. Jeffrey J. Early, Gerardo Hernández-Dueñas, Leslie M. Smith & M.-Pascale Lelong. Exact expressions for available potential energy and available potential vorticity.
Extended abstracts:

A Scheme for Shallow Water Flow with Area Variation.
Smadar Karni and G. Hernández-Dueñas.
American Institute of Physics.
AIP Conference Proceedings
International Conference on Numerical Analysis and Applied Mathematics
Rethymno, Crete, Greece, 18-22 September 2009. 1168 (2009), 1433-1436.
Link to Journal


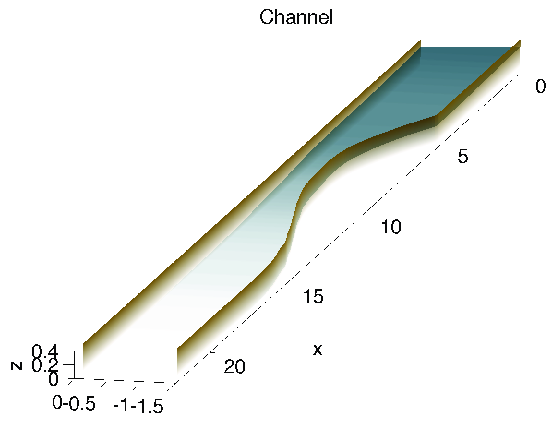 A central-upwind scheme with artificial viscosity for shallow-water flows in channels. Advances in Water Resources 96 (2016) 323-338.
A central-upwind scheme with artificial viscosity for shallow-water flows in channels. Advances in Water Resources 96 (2016) 323-338.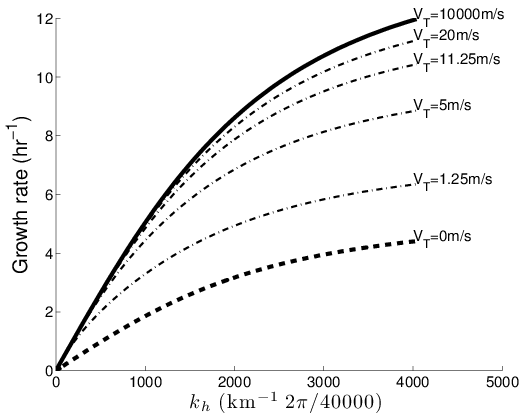 8. G. Hernandez-Duenas, Leslie M. Smith, and Samuel N. Stechmann. Stability and instability criteria for idealized precipitating hydrodynamics. Journal of Atmospheric Sciences, Vol 72, No. 6 (2015), pp. 2379-2393.
8. G. Hernandez-Duenas, Leslie M. Smith, and Samuel N. Stechmann. Stability and instability criteria for idealized precipitating hydrodynamics. Journal of Atmospheric Sciences, Vol 72, No. 6 (2015), pp. 2379-2393.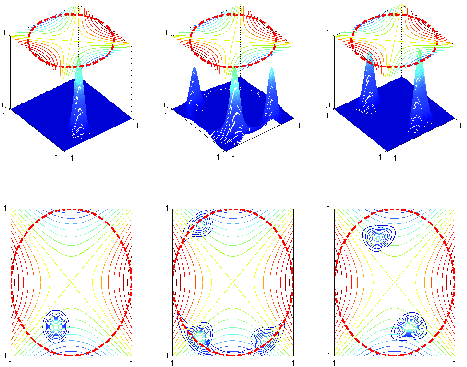 7. G. Hernandez-Duenas and Alejandro Uribe. Algebras of semiclassical pseudodifferential operators associated with Zoll-type domains in cotangent bundle. Journal of Functional Analysis, 268 no. 7 (2015), pp. 1755-1807.
7. G. Hernandez-Duenas and Alejandro Uribe. Algebras of semiclassical pseudodifferential operators associated with Zoll-type domains in cotangent bundle. Journal of Functional Analysis, 268 no. 7 (2015), pp. 1755-1807.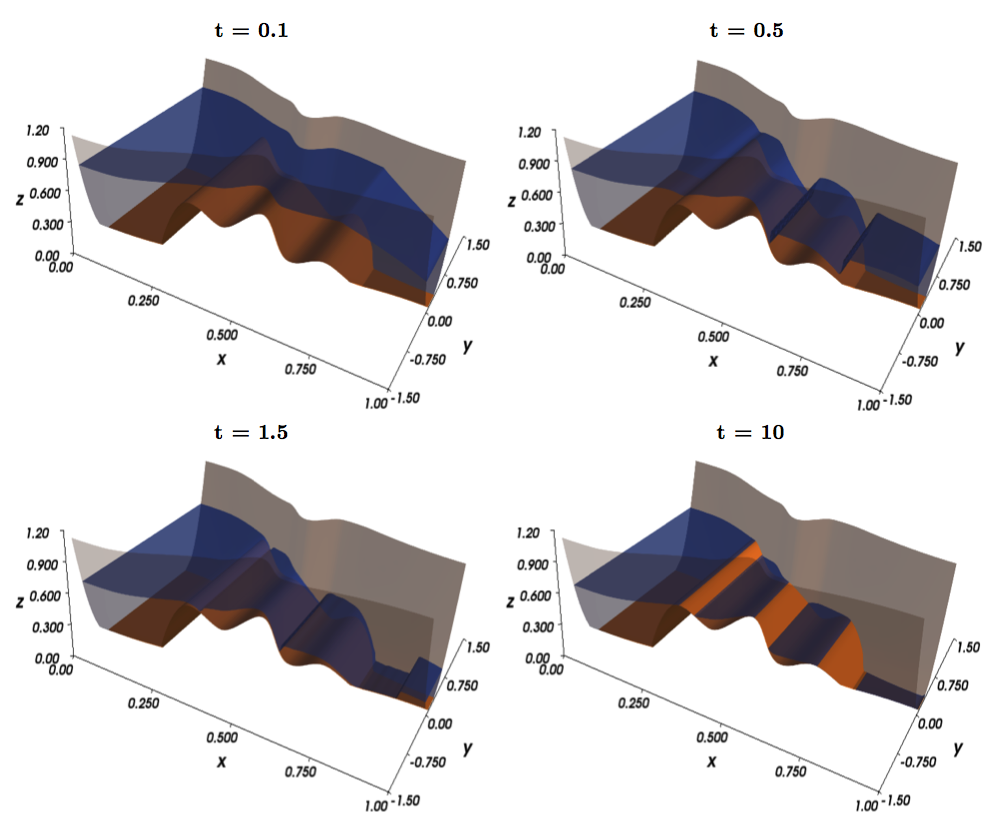 6. Jorge Balbás and G. Hernandez-Duenas. A Positivity Preserving Central Scheme for Shallow Water Flows in Channels with Wet-Dry States. ESIAM: Mathematical Modelling and Numerical Analysis (M2AN) 48 (2014) 665-696.
6. Jorge Balbás and G. Hernandez-Duenas. A Positivity Preserving Central Scheme for Shallow Water Flows in Channels with Wet-Dry States. ESIAM: Mathematical Modelling and Numerical Analysis (M2AN) 48 (2014) 665-696.
 and Waves in Geophysics. Springer (Book) (1), pp 1-195 (2022).
and Waves in Geophysics. Springer (Book) (1), pp 1-195 (2022).


 ensional shallow water flows in open channels with varying width
ensional shallow water flows in open channels with varying width