PDERBF

Radial Basis

Function Methods

for the Solution of Partial Differential Equations

Comenzar Get Started Commencer
Institutions

About..

The main purpose of the research project: Radial Basis Function Methods for the Solution of PDE, is to study, research and develop numerical algorithms to solve partial differential equations by means of radial basis function methods. These techniques, which were developed during the last decade, have proved to be a powerful tool for the solution of real life problems of great scale.

This project is essentially interdisciplinary; we aim to build mathematical models of problems, which belongs to different areas of knowledge. An important objective of this project is to develop a flexible, object oriented library, which let the user to apply and implement these numerical techniques. Our purpose, is not only to use “black boxes” to solve PDE problems, but instead, to boost the implementation and developement of computational systems for these new methods

This project has tree main objectives, which can be classified into: research, education and computer systems development:

  • 01 Research:

    In the field of research, we aim to investigate numerical algorithms both form the theoretical and applied point of view. The application of these techniques to different areas of knowledge is also an important purpose of this point.

  • Within the educational objective, we incorporate simple codes as well as their explanation, which aims to help students and lecturers to understand and/or teach these new numerical methods.

  • The third objective is to build a free software library whose flexibility let the user to incorporate new routines or algorithms.

 

Numerical Methods for the Solution of Partial Differential Equations: A Review

(Métodos Numéricos para la Solución de Ecuaciones Diferenciales Parciales: una crítica)

Research

Radial Basis Functions for Solving EDP: Introductory note:

  • → General Comments:

    Despite the fact that radial basis functions methods are relatively new (they were first formulated during the beginning of the 90's), its impact on science and engineering is already remarkable (for example [I,II,III,IV, V, VI] and the references therein). Their effectiveness and success is a result of their meshless formulation. When working with real world problems it is frequent to use 70% of the processing time generating the meshes necessary for the numerical method to be used. Given this background we highlight some points that make these methods more powerful than classical methods:

    None of this methods call for the use of meshes, immediately reducing the computational cost of the algorithm. It is simple to refine the number of nodes in regions where the function oscillates or the gradient misbehaves. Adaptive nodes techniques are less expensive than adaptive mesh methods.

  • Handling problems in more than two dimensions or with a complex boundary shape is more simple and more efficient that with mesh-dependent methods. There are several ways in which radial basis function methods for solving partial differential equations can be classified. We can use the following two categories classification:
    • Radial basis function methods that are:
    → Global methods
    → Local methods
    • Mobile least squares methods.

  • The distinguishing factor is the order of convergence. With radial basis function methods the order of convergence depends on the type of kernel used ,while mobile least squares methods posses a polynomial convergence rate that depends on the specific kernel being used.

    Another mayor difference is that radial basis function methods are not independent of the dimension of the space, these methods pose the same algebraic system -the Gramm matrix- when working with one, two or more space dimensions. Opposed to this mobile least squares methods' complexity depends on the dimension of the euclidean space we are working on.

    On the one hand global radial function methods treatment turns into the solution of an system of algebraic equations that take into account all nodes in the domain, in the meanwhile least squares methods again give us a smaller algebraic equations system where only some nodes are taken into account.

  • When dealing with global radial function methods one of the principal problems we face is that the condition number of the matrix raised from the set of equations posed by the problem grows with the number of nodes used. This pathology is not found when working with MLS , given that local systems require the solution of diagonally dominant band matrices. However, local methods can not give us exponentially convergent schemes, while global methods are suited for such duty. Additionally for global methods there have been preconditioning techniques that allow handling a large number of nodes.

  • Both categories have had repercussion in different disciplines and their ability for solving an assorted range of problems is subject of active research. Among the most significant methods of both categories we find:
    Radial basis function methods:
    • Symmetric and asymmetric collocation methods.
    • Differential quadrature.
    • Radial compact supported basis functions.
    • Fundamental solutions methods.

    Mobile least squares methods:
    • Petrov Galerkin sin mallas (MLPG)
    • Partition of unity finite elements (PUFEM)
    • Partition of unity reproductive kernels (RKPM)
    • Smooth particle hydrodinamics (SPH).

  • Recently Fasshauer [VII] introduced an abstract formulation that unifies both categories -when using radial kernels- under a common framework. In particular the author showed that local methods obtained from using mobile least squares can be transformed into global methods when the number of nodes contained in the support of local techniques constitute the entire set of nodes in the domain.


    [I] S. N. Atluri and S. Shen, The Meshless Local Petrov-Galerkin (MLPG) Method, Tech Science Press, Encino, CA, 2002.
    [II] M. D. Buhmann, Radial Basis Functions : Theory and Implementations, Cambridge University Press, Cambridge, 2003.
    [II] E. W. Cheney and W. A. Light, A Course in Approximation Theory, Brooks/Cole, Pacific Grove, CA, 1999.
    [IV] G. R. Liu, Mesh Free Methods: Moving beyond the Finite Element Method, CRC Press, Boca Raton, FL, 2002.
    [V] Wendland, H., Scattered Data Approximation, Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press, Cambridge, UK., 2005
    [VI] G. E. Fasshauer, Meshfree Approximation Methods with Matlab Interdisciplinary Mathematical Sciences - Vol. 6 World Scientific Publishers, Singapore, 2007
    [VII] G. E. Fasshauer, Dual Bases and Discrete Reproducing Kernels: A Unified Framework for RBF and MLS Approximation, Engineering Analysis with Boundary Elements, Volume 29, Issue 4, April 2005, pages 313-325

  • The former methods have had a significant impact in other disciplines. We mention some few select examples:
    1. Quantitative Finance
    Black–Scholes equation is constantly used for modeling the price of some financial products. Models for the price of American and European options using RBF have been proposed and studied by Hon et al. [1,2], and in the one and two dimensional setting by Fasshauer et al [3] and by Marcozzi et al. [4]. Hon formulated a method based in quasi-radial functions in one dimension. Recently Pettersson et al. [6] solved the multidimensional problem for the European Basket call option using a multi quadratic kernel and adaptive nodes while reporting an acceleration by a factor of 20 to 40 times with respect to finite difference methods.

    [1] Y.-C. Hon, X.-Z. Mao, A radial basis function method for solving options pricing models, J. Financial Engineering 8 (1999) 31–49.
    [2] Z.Wu, Y.-C. Hon, Convergence error estimate in solving free boundary diffusion problem by radial basis functions method, Engrg. Anal. Bound. Elem. 27 (2003) 73–79.
    [3] G. E. Fasshauer, A. Q. M. Khaliq, D. A. Voss, Using meshfree approximation for multi-asset American option problems, J. Chinese Institute Engineers 27 (2004) 563–571.
    [4] M. D. Marcozzi, S. Choi, C. S. Chen, On the use of boundary conditions for variational formulations arising in financial mathematics, Appl. Math. Comput. 124 (2001) 197–214.
    [5] Y. C. Hon, A quasi-radial basis functions method for American options pricing, Comput. Math. Appl. 43 (3) (2002) 513–524.
    [6] Ulrika Pettersson, Elisabeth Larsson, Gunnar Marcusson, and Jonas Persson, Improved Radial Basis Function Methods for Multi-Dimensional Option Pricing, Technical Report 2006-028, Uppsala University, 2006.

  • In [7] N. Flyer et al. attack the problem of modeling fluxes in a sphere, dominated by convective terms. This is the first time RBF methods are used to solve a hyperbolic equation. The authors point out that the amount of nodes used with this method is less than the number of nodes used during spectral methods calculations. In addition to this RBF methods allow to use bigger time steps than the steps used in spectral methods.
    In Jichun Li [8] , Hon [9] y Wong et al. [10] shallow water equations are solved using the asymmetric collocation method via a multi quadratic kernel. In [20] a study for Tolo's harbor in Hong Kong, where these new methods are compared with finite element techniques and field data, is considered, obtaining superior results to the FE methods and agreeing with field data remarkably.
    [7] N. Flyer and G.B. Wright, Transport schemes on a sphere using radial basis functions. J. Comp. Phys., to appear (2007).
    [8] Jichun Li, C.S. Chen, Darrel Pepper, Yitung Chen, "Mesh-free method for groundwater modeling", Boundary Elements XXIV, eds. C.A. Brebbia, A. Tadeu and V. Popov, WIT Press, Southampton, Boston, pp. 115-124 (2002).
    [9] Y. C. Hon, K. F. Cheung, X. Z. Mao, and E. J. Kansa, .A Multiquadric Solution for Shallow Water Equations", ASCE J. Hydraulic Engineering, 125, (5), 524-533 (1999).
    [10] Wong, S. M., Hon, Y. C., and Golberg, M. A. 2002. Compactly supported radial basis functions for shallow water equations. Appl. Math. Comput. 127, 1 (Mar. 2002), 79-101
    Modeling two-phase and three-phase fluxes is done by Hon in [11] and [12] using an Eulerian asymmetric collocation formulation and using multi quadratic kernels. A. Iske et al. [13] [14] worked the same problem developing a semi-lagrangian method that uses thin layer kernels for solving Buckley-Leverett equations, towards the modeling of two-phase problems arising from the oil industry.
    [11] Y. C. Hon, M. W. Lu, W. M. Xue, and X. Zhou, "Multiquadric Method for the Numerical Solution of a Biphasic Model", Internat. J. Appl. Sci. Comput., 88, 153-175 (1997).
    [12] Y. C. Hon , M. Lu , M. W. Xue and X. Zhou, "Numerical Algorithm for Triphasic Model of Charged and Hydrated Soft Tissues", Computacional Mechanics, 29(1), , pp 1-15 (2002)
    [13] A. Iske and M. Käser: Two-Phase Flow Simulation by AMMoC, an Adaptive Meshfree Method of Characteristics. Computer Modeling in Engineering & Sciences (CMES) 7(2), 2005, 133-148.
    [14] J. Behrens, A. Iske, and M. Käser: Adaptive Meshfree Method of Backward Characteristics for Nonlinear Transport Equations, in Meshfree Methods for Partial Differential Equations, M. Griebel and M. A. Schweitzer (eds.), Springer-Verlag, Heidelberg, 2002, 21-36.
    Chen et al. [15] estudian la modelación del transporte de contaminantes para yacimientos de agua mediante técnicas de colocación con RBF. El estudio numérico incluye varios casos: difusión pura, advección y dispersión para una fuente continua, advección y dispersión para una fuente instantánea.
    [15] J. Li, Y. Chen and D. Pepper, Radial basis function method for 1-D and 2-D groundwater contaminant transport modeling, Computational Mechanics, (32) 10-15, 2003

  • Navier Stokes solution, either for the stationary or for the time-dependent cases was studied by Shu, et al. [16] [17] [18],
    [16] Shu, C., Khoo, B. C., and Yeo, K. S. 1994. Numerical solutions of incompressible Navier—Stokes equations by generalized differential quadrature. Finite Elem. Anal. Des. 18, 1-3 (Dec. 1994), 83-97.
    [17] C. Shu, H. Ding and K. S. Yeo (2005), 'Computation of incompressible Navier-Stokes equations by local RBF-based differential quadrature method', CMES-Computer Modeling in Engineering and Sciences, 7, 195-205.
    [18] H. Ding, C. Shu, K. S. Yeo and D. Xu (2006), 'Numerical Computation of Three-dimensional Incompressible Viscous Flows in the Primitive Variable Form by Local Multiquadric Differential Quadrature Method', Computer Methods in Applied Mechanics and Engineering, 195, 516-533.
    Chinchapatnam et al. [19] study the non-stationary convection- diffusion equation in one and two dimensions for different Peclet numbers using symmetric and asymmetric collocation. The numerical scheme uses global radial basis functions, such as multi quadratic kernels and thin layer splines. During this study the authors conclude that the symmetric method is just marginally better than the asymmetric method and that for large Peclet numbers high node density is required for a proper approximation.
    [19] Chinchapatnam, P.P., Djidjeli, K and Nair, P.B. (2006). Unsymmetric and symmetric meshless schemes for the unsteady convection–difusión equation. Computer Methods in Applied Mechanics and Engineering, 195, (19-22), 2432-2453.

  • As far as we know there are not many references on radial basis functions of the global type for structural analysis. It is worth mention the work of Ferreira et al. [20] for stress in steel beams, the work of Zhang et al. [21] for planar elasticity. Recently Tiago et al. [22] use the asymmetric collocation method for several radial kernels in order to solve and analyze one dimensional problems ranging from static linear elasticity, free vibration and linear stability analysis to physical non-linear problems.
    [20] A. J. M. Ferreira, C. M. C. Roque, and P. A. L. S. Martins. Radial basis functions and higher-order shear deformation theories in the analysis of laminated composite beams and plates. Composite Structures, 66(1–4):287–293, 2004.
    [21] X. Zhang, K. Z. Song, M. W. Lu, and X. Liu. Meshless methods based on collocation with radial basis functions. Computational Mechanics, 26(4):333–343, 2000.
    [22] C. Tiago and V. Leitão, Application of radial basis functions to linear and non-linear structural analysis problems, Computers & Mathematics with Applications, 51(8), 1311-1334, 2006.

A state of the art in radial basis function methods:

  • - Review articlen:

    RBFs Methods for the Solution of PDE.

  • • Symmetric and non symmetric collocation methods.
    • Differential Quadrature.
    • Galerkin.
    • Preconditioning methods.
    • Domain decomposition.
    → Overlapping algorithms.
    → Non-overlapping algorithms.
    •Node adaptive algorithms.
    → Local algorithms.
    → Global algorithms.
    • Visualization of the solutions.

  • Biphasic inmiscible flow. Buckley Leverett equation.
    Radial basis function method for ground water contaminant transport modeling.

 
-Biophasic inmiscible flow. Buckley Leverett equation
C ++ library
Radial Basis Function - UNAM
Problems library Radial Basis Function
RBF++
Problems library Radial Basis Function RBF++ Documentaction Ver. 1.0 May 2008 UNAM
UNAM

As mentioned in the main, an important objective of this project is to build a software library that enables the implementation of algorithms for radial basis functions for the solution of the PDE. An important objective here is that the user to include in a friendly manner new routines and modules through oriented based on the C ++ objects strategy.
The library is currently at an early stage, kindly invite software developers interested in this area, incorporating object-oriented modules following the approach of free software (GPL). Please contact Daniel A. Cervantes to any matter relating to this library,dcchivela@gmail.com.

Documentación
Classes
Files
A different software package can be found in:
Templates Units for Numerical Applications: Radial Basis Functions.
Reference Manual
TUNA::RBF
Class List
Radial Basis Function Library for PDEs Problems
RBF++
Documentation Ver. 1.0 May 2008
UNAM
Class List
LA::Matrix Base class for matrices
LA::Point Base class for Points
LA::Point2dT Class for two dimension points
LA::Point3dT Class for three dimension points
RBF::GramMatrix Gram matrix class
RBF::MQ Multicuadric kernel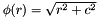
RBF::TPS2 Second order thin plate spline kernel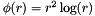
RBF::TPS4 Fourth order thin plate spline kernel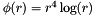
RBF::TPS_2DX Second order partial derivative of thin plate spline (with respect to )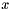
RBF::TPS_2DY Second order partial derivative of thin plate spline (with respect to )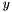
RBF::TPSInterp Thin plate spline interpolator class
Lista de Archivo
Radial Basis Function Library for PDEs Problems
RBF++
Documentation Ver. 1.0 May 2008
UNAM
File List 
    
RBF++-0.1/examples/linear_alg/linear_alg.cpp [code]	 
RBF++-0.1/examples/tps_interpolation/tps_interpolation.cpp [ code]	 
RBF++-0.1/examples/tps_poisson/tps_poisson.cpp [code]	 
RBF++-0.1/include/LA/Matrix.h [code]	 
RBF++-0.1/include/LA/Point.h [code]	 
RBF++-0.1/include/LA/Point2dT.h [code]	 
RBF++-0.1/include/LA/Point3dT.h [code]	 
RBF++-0.1/include/RBF/GrammMatrix.h [code]	 
RBF++-0.1/include/RBF/RBF.h [code]	 
RBF++-0.1/include/RBF/TPSInterp.h [code]	 
RBF++-0.1/src/LA/Matrix.cpp [code]	 
RBF++-0.1/src/LA/Point.cpp [code]	 
RBF++-0.1/src/RBF/GrammMatrix.cpp [code]	 
RBF++-0.1/src/RBF/TPSInterp.cpp [code]

Meteorología y Geofísica:

In [7], N. Flyer et al. propose the problem of modelling geophysical fluids on a sphere dominated by convective terms. It is the first work in which hyperbolic partial differential equations are solved by radial basis functions. The authors report that the number of required nodes is much lower than when using spectral methods. Furthermore, the RBF method allows much larger timesteps than the ones employed by the same classical spectral methods.

Jichun Li [8] , Hon [9] y Wong et al. [10] solve the shallow water equations via asymmetric collocation with multiquadric kernels. In particular, in [20] a study of Tolo Harbour in Hong Kong is developed which is compared with finite element methods and field data, yielding technical superiority over FEM and an excellent agreement with field data.
[7] N. Flyer and G.B. Wright, Transport schemes on a sphere using radial basis functions. J. Comp. Phys., to appear (2007).
[8] Jichun Li, C.S. Chen, Darrel Pepper, Yitung Chen, "Mesh-free method for groundwater modeling", Boundary Elements XXIV, eds. C.A. Brebbia, A. Tadeu and V. Popov, WIT Press, Southampton, Boston, pp. 115-124 (2002).
[9] Y. C. Hon, K. F. Cheung, X. Z. Mao, and E. J. Kansa, .A Multiquadric Solution for Shallow Water Equations", ASCE J. Hydraulic Engineering, 125, (5), 524-533 (1999).
[10] Wong, S. M., Hon, Y. C., and Golberg, M. A. 2002. Compactly supported radial basis functions for shallow water equations. Appl. Math. Comput. 127, 1 (Mar. 2002), 79-101
Hon [11,12] works with two-phase and three-phase fluid modelling with an Eulerian approach and multiquadric asymmetric collocation. Iske et al. [13, 14] tackle the same problem developing a semi-lagrangian method that uses thin-plate kernels to solve Buckley-Leverett equations, aiming to model two-phase problems applicable to the primary recovery of wells in the oil industry.

[11] Y. C. Hon, M. W. Lu, W. M. Xue, and X. Zhou, "Multiquadric Method for the Numerical Solution of a Biphasic Model", Internat. J. Appl. Sci. Comput., 88, 153-175 (1997).
[12] Y. C. Hon , M. Lu , M. W. Xue and X. Zhou, "Numerical Algorithm for Triphasic Model of Charged and Hydrated Soft Tissues", Computacional Mechanics, 29(1), , pp 1-15 (2002)
[13] A. Iske and M. Käser: Two-Phase Flow Simulation by AMMoC, an Adaptive Meshfree Method of Characteristics. Computer Modeling in Engineering & Sciences (CMES) 7(2), 2005, 133-148.
[14] J. Behrens, A. Iske, and M. Käser: Adaptive Meshfree Method of Backward Characteristics for Nonlinear Transport Equations, in Meshfree Methods for Partial Differential Equations, M. Griebel and M. A. Schweitzer (eds.), Springer-Verlag, Heidelberg, 2002, 21-36.
Chen et al. [15] study groundwater contaminant transport modellingvia RBF collocation techniques. Their numerical study incluces various cases: pure diffusion, advection, and dispersion for a continuous source; advection and dispersion for an instantaenous source.
[15] J. Li, Y. Chen and D. Pepper, Radial basis function method for 1-D and 2-D groundwater contaminant transport modeling, Computational Mechanics, (32) 10-15, 2003


Fluids Dynamics:

The solution to the Navier-Stokes equations, both stationary and time-dependent, has been attacked by Shu et al. [16] [17] [18], in which they solve the problem for a square cavity, Ghia, with the differential quadrature method for Reynolds numbers above 10^5.
[16] Shu, C., Khoo, B. C., and Yeo, K. S. 1994. Numerical solutions of incompressible Navier—Stokes equations by generalized differential quadrature. Finite Elem. Anal. Des. 18, 1-3 (Dec. 1994), 83-97.
[17] C. Shu, H. Ding and K. S. Yeo (2005), 'Computation of incompressible Navier-Stokes equations by local RBF-based differential quadrature method', CMES-Computer Modeling in Engineering and Sciences, 7, 195-205.
[18] H. Ding, C. Shu, K. S. Yeo and D. Xu (2006), 'Numerical Computation of Three-dimensional Incompressible Viscous Flows in the Primitive Variable Form by Local Multiquadric Differential Quadrature Method', Computer Methods in Applied Mechanics and Engineering, 195, 516-533.
Chinchapatnam et al. [19] investigate the transient convection-diffusion equation in one and two dimensions for different Péclet numbers using symmetric and unsymmetrical collocation. The numerical scheme uses global radial functions, such as multiquadrics, inverse multiquadrics, thin plate splines, and quintics. In this comparative study, the authors conclude that the symmetric method is only marginally better than the unsymmetric method, and that for large Péclet numbers a high node density is required to achieve a good approximation.
[19] Chinchapatnam, P.P., Djidjeli, K and Nair, P.B. (2006). Unsymmetric and symmetric meshless schemes for the unsteady convection–difusión equation. Computer Methods in Applied Mechanics and Engineering, 195, (19-22), 2432-2453.


Elasticity and Structural Analysis

There are few references, to the best of our knowledge, on global radial basis function methods for solving structural analysis problems.. We must highlight, however, the work of Ferreira et al. [20] that deals with the strain problem for beams and deformable composite plates, as well as the work of Zhang et al. [21] in planar elasticity. Recently Tiago et al. [22] use the method of unsymmetric collocation with various radial kernels to solve and analyse one-dimensional problems ranging from static linear elasticity, free vibrations, and linear stability analysis, to nonlinear physical problems of damaged models.
[20] A. J. M. Ferreira, C. M. C. Roque, and P. A. L. S. Martins. Radial basis functions and higher-order shear deformation theories in the analysis of laminated composite beams and plates. Composite Structures, 66(1–4):287–293, 2004.
[21] X. Zhang, K. Z. Song, M. W. Lu, and X. Liu. Meshless methods based on collocation with radial basis functions. Computational Mechanics, 26(4):333–343, 2000.
[22] C. Tiago and V. Leitão, Application of radial basis functions to linear and non-linear structural analysis problems, Computers & Mathematics with Applications, 51(8), 1311-1334, 2006.

Teaching

Numerical methods for the solution of EDP by radial basis function.

NEW: Advanced Postgraduate Course in Mathematics, UNAM, 2019

Course Notes:

↗ Introduction to the Theory of Radial Functions

↗ Numerical methods for the solution of EDP by radial basis function.

Numerical Algorithms: explanation of codes.

→Interpolation by radial functions.

→Solution of the Poisson equation.

→Solution of the equation of convective diffusion.

→Domain decomposition with radial functions.

Programming Issues

*Introduction to Programming with C ++

*Object oriented programming.

*Generic programming.

*Parallel Programming (MPI).

*Templates for the solution of linear systems.

*Tips for managing Joomla.

*How to create a new page in Joomla



Codes in matlab and C ++
Programs surface interpolation.

Surface Interpolation from Random Data

Algorithm
Interpolation using radial functions.
Interpolation from Thin Plate: Codes in Matlab

Main program
Main Program and Auxiliary Routines (compressed)

Interpolation from Thin Plate: Codes in C++
Main Program
Main Program and Auxiliary Routines (compressed)/a>

Programs to solve the convection diffusion equation

Convection Diffusion
Pure 2-D Convection, using non-symmetrical placement.
Matlab
Main routine

Main and auxiliary routine (compressed)

C++
Ut + Ux + Uy =0

Main routines
Explicit method, TPS+Pol grade 6

Implicit TPS+Pol method grade 6

Explicit method Multiquadratic Kernel

Main and auxiliary routine (compressed)

Convection - 2-D diffusion, using non-symmetrical placement.
Matlab
Main routine

Main and auxiliary routine (compressed)

C++
Ut + mu*(Ux + Uy) = beta*grad(U)

Main routines
Implicit method, TPS + Pol grade 6

Implicit Multiquadric Nucleus Method

Main and auxiliary routine (compressed)

Notice to students:

Announcement

Undergraduate and postgraduate students are invited to graduate by solving problems described in terms of EDPs using parallel computing techniques and radial basis functions, as well as by using the library developed from this project.

For Undergraduate and Postgraduate thesis topics, please contact Dr. Pedro González Casanova, (Instituto de Matemáticas, UNAM).
TEL: 56 22 47 47, or email: casanova@matem.unam.mx

Recommended readings:
→ Wendland, H., Scattered Data Approximation, Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press, Cambridge, UK., 2005
→ G. E. Fasshauer, Meshfree Approximation Methods with Matlab Interdisciplinary Mathematical Sciences - Vol. 6 World Scientific Publishers, Singapore, 2007

Interested students Contact: The academics participating in this project


Members

Académics:

Dr. Pedro González Casanova Henríquez

Project coordinator:

Instituto de Matemáticas, UNAM

Dr. Dominique Apprato

(project Ecos Nord)

Université de Pau et des Pays de l'Adour | UPPA · Mathématiques Appliquées

Dr. Mohammed-Najib Benbourhim,

(Research-gate)

(Paul Sabatier University - Toulouse III, Toulouse, France).

Dr. Daniel Cervantes Cabrera

INFOTEC CDMX

Dr. Luis Miguel de la Cruz Salas,

Instituto de Geofísica, UNAM

Dr. Christian Gout,

(Laboratoire de Mathématiques de l'INSA de Rouen, EA 3226, France)

Dr. Jose Antonio Muñoz Gómez,

CUCSUR, Universidad de Guadalajara

Dr. Gustavo Rodríguez Gómez,

INAOE

Students:

Doctorate:

  • Doctoral thesis of Daniel Cervantes Cabrera, (UNAM), marzo de 2017.
  • M. en C. Jorge Zavaleta Sánchez,(UNAM)

Mastery:

  • Anthony Torres Hérnandez, (UNAM)
  • Louis David Bretón Tenorio, (UNAM)
  • Clémentine Cavaroc (INSA de Rouen, France)
  • José Rodrigo Rojo García, (UNAM)

Publications

D. Cervantes, P. Gonzalez Casanova, C. Gout, L. H. Juarez, R. Resendiz, Vector field approximation using radial basis functions, Journal of Computational and Applied Mathematics, Ed. Elsevier, Volume 240, 1 March 2013, Pages 163–173. R. Reséndiz, L. H. Juárez, P. González-Casanova, D. A. Cervantes, C. Gout, Numerical Study of Wind Field Adjustment with Radial Basis Functions, Environmental Science and Engineering, Ed. Springer, 2013, Part 4, 371-378. P. González-Casanova, J. Antonio Muñoz-Gómez, G. Rodríguez-Gómez, Node Adaptive Domain Decomposition Method by Radial Basis Functions. Journal of Numerical Methods for Partial Differential Equation , Volume 25 Issue 6, Pages 1482 - 1501, 2009. J. Antonio Muñoz-Gómez, P. González-Casanova, G. Rodríguez-Gómez, "Exponential Convergence of Multiquadric Collocation Method: a Numerical Study". Revista de Ingeniería, Investigacion y Tecnologia, Issue 3, pages 197-206, 2009. V. Pereyra, G. Scherer, P. Gonzalez Casanova, Radial function collocation solution of partial differential equations in irregular domains , International Journal of Computing Sciences and Mathematics, Vol. 1, No. 1, 2007. D. Cervantes, P. Gonzalez-Casanova, C. Gout, Seafloor surfaces approximation from rapidly varying bathymetric data using pre-processing, Pages 1742 - 1744, IEEE Transaction on Geosciences and Remote sensing, 2007. J. Antonio Muñoz-Gómez, P. González-Casanova, G. Rodríguez-Gómez, Domain Decomposition by Radial Basis Functions for Time Dependent Partial Differential Equations, Proccedings of the IASTED: International Conference on Advances in Computer Science and Technology, pp. 105-109, (2006). J. Antonio Muñoz-Gómez, P. González Casanova, G. Rodríguez-Gómez, Adaptive Node Refinement Collocation Method for Partial Differential Equations, ENC-06 Sixth Mexican International Conference on Computer Sciences, published by IEEE, pp 70-77, (2006). P. González-Casanova, C. Gout, Approximation Near the Boundary of a Radial Quasi interpolant in Polygonal Domains , Int. J. of Comp. Math. 81 (12), pp. 1145-1455 (2004). González-Casanova, Pedro. A Hilbertian approach to quasi-interpolation methods. Neural Parallel Sci. Computations, 5 (1997), no. 1-2, 257--274. Benbourhim, M. N.; González-Casanova, P. Generalized variational quasi interpolants in $(H\sp m\sb O(\Omega))\sp n$. Bol. Soc. Mat. Mexicana, 3 (1997) , no. 2, 347--354. Benbourhim and P. González Casanova,. Local Interpolation of non smooth functions , Proceedings of the Thirth International Conference on Approximation and Optimization, Puebla, México 1995, European Matematical Society, Electronic Library of Mathematics, en Julio de (1997). González-Casanova, Pedro; Wolf, Kurt Bernardo. Interpolation for solutions of the Helmholtz equation. Numer. Methods Partial Differential Equations ,11 (1995), no. 1, 77--91. Atteia M., Benbourhim M. N., González Casanova P. Quasi-interpolant Elastic Manifolds. Reporte de Investigación IIMAS-UNAM, Vol. 3, No. 25, (1993) . González Casanova P. and Álvarez R. Splines in Geophysics. Golden Anniversary Issue, Geophysics. Vol. 50 No. 12, December 1985. pp. 2831-2848.

Activities

33rd International Conference on Boundary Elements and other Mesh Reduction Methods

28 - 30 June 2011, New Forest, UK

Marcos Capistran

Lecture on Black Scholes and Radial Basis Functions, ENOAN 2010

Pan-American Advanced Studies Institute in Computational Science and Engineering.

A summer institute held 3–14 January 2011, Valparaiso, Chile

Fourth International Conference on Multivariate Approximation:

Theory and Applications at Cancun, Mexico April 26 - May 01, 2007

Second Latin American SCAT Workchop,

Island Cozumel, México, November 2007.

Ninth International Conference 'Approximation and Optimization in the Caribbean´

Andres Island, Colombia- March 2-7, 2008

Mathematical and Computational Modeling Seminar

Instituto de Geofísica de la UNAM

Internal seminars:

TUNA::RBF. Dr. Luís Miguel de la Cruz, 28 de agosto 2008. Lugar: DGSCA.


Using patterns for scientific software design
Dr. Gustavo Rodríguez Gómez, 4 de septiembre 2008. Lugar: DGSCA.

Enlaces

Robert Schaback Wendland Bengt Fornberg Greg Fasshauer Armin Iske Martin Buhmann Jeremy Levesley's R. Schaback's research group Carsten Franke: Scientific links Carl de Boor Amos Ron Christian Gout Rodrigo B. Platte Toby Driscoll Victor Pereyra Cheng, A.H.-D Joseph D. Ward